February 11, 2005 2:59 AM
The factorial of a number increases rapidly with the number. 10! is
exactly the number of seconds in six weeks; 11! exceeds the number of
seconds in one year whereas 12! exceeds the number of seconds in 12
years.
To approximately get an idea of the factorial of a very large number, we can use the formula devised by James Stirling1:
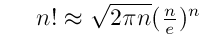
The relative error introduced to the actual value by this formula is approximately 1/(12n).
8! according to this formula is approximately 39902 when the actual value is 40320.
Stirling also tried to generalize n! to noninteger n. The results led
to an infinite sequence to represent ln n!2.
Leonardo Pisano3 published the famous Fibonacci sequence:
0, 1, 1, 2, 3, 5, 8, 13, ...,
which can be represented as a recurrence relation of the form:
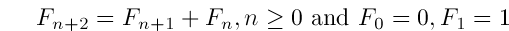
whose solution to Fn is:
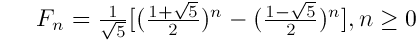
[1] In his famous work Methodus Differentialis (1730).
[2] More about this at Stirling's Approximation.
[3] Also known as Leonardo Fibonacci.